MONDAY, MONDAY: La insondable sabiduría de Pí

 Ya el lunes pasado, en la sección «MONDAY, MONDAY» de este blog, publicamos una nota sobre el enigmático número Pí, sobre la cual recibimos diversos comentarios, todos muy positivos. Pero destaca entre ellos, en gran medida, este notable ensayo,  que reproducimos  con entusiasmo y alegría, por sus indudables méritos. Fue publicado originalmente en «CATRECITO», un blog que no dudamos en recomendar,  que aparece en el diario colombiano EL ESPECTADOR (enlace al final del ensayo).

Marcos Villasmil

—————–

Un hermoso y profundo artículo sobre el número Pí, de Antonio Vélez.

Advertencia: En este ensayo aparecen conceptos, fórmulas y símbolos matemáticos que pueden desanimar al lector no especializado. Sin embargo, no es necesario entenderlos para comprender las ideas esenciales. Más aún, debido a su belleza abstracta, algunas de las fórmulas se presentan únicamente para ser contempladas.

Este misterioso 3,1415…, que se cuela por todas las puertas y ventanas, que se desliza por cualquier chimenea. 

Augustus de Morgan.

Ninguno de los números conocidos por el hombre ha recibido más atención individual que Pí. La lucha por conocerlo, esto es, la búsqueda de sus cifras decimales, ha sido una competencia abierta que empezó por allá en la época de los faraones con los dos primeros dígitos, fue ampliada a cuatro por los griegos de la Antigüedad, y hoy se han sobrepasado los cincuenta mil millones y apenas se está comenzando. Quizá la competencia no termine nunca. El conocimiento de Pí, como se verá, es una empresa sobrehumana: tuvo principio pero no tendrá fin.

La fascinación que suscita, inexplicable para algunos, ha hecho que muchos hombres, en todas las épocas y en todos los idiomas, se hayan ocupado de él. Se han dicho cosas serias y profundas, y también divertidas y banales. Su historia es larga, tachonada de amenas anécdotas y de hechos curiosos. Con el dudoso fin didáctico de aprender de memoria sus primeras cifras decimales, se han compuesto versos de centavo, como los que siguen a continuación, atribuidos a un colombiano, R. Nieto París:

Soy Pí lema y razón ingeniosa

de hombre sabio que serie preciosa

valorando enunció magistral.

Con mi ley singular bien medido

el amplio orbe por fin reducido

fue al sistema ordinario cabal.

Allí aparece nuestro número disfrazado o codificado en forma alfabética. Basta cambiar cada palabra del texto por el número de sus letras, para que al lector se le revele el valor de pí con sus primeras treinta y una cifras decimales.

Han existido fenómenos humanos de memoria de gran fondo que le han rendido honores, como fue el caso de Hans Eberstark, austríaco nacido en 1929, experto en traducción simultánea y cálculo mental. Dominaba este portento quince lenguas y conocía de memoria las primeras doce mil cifras de pí. Es posible que ahora el japonés Hideaki Tomoyori posea la marca mundial en esta especialidad: sin avergonzarse lo más mínimo, ha logrado recitar de memoria las primeras veinte mil cifras decimales del famoso número.

Puede asegurarse, además, que casi ningún campo de la ciencia puede ignorarlo. Aparece sin anunciarse en los puntos más insólitos, como si poseyera el don de la ubicuidad científica. En fin, tal como se verá enseguida, es voluminosa y densa la historia del descubrimiento de pí, y la de la conquista de sus propiedades. Pero igualmente voluminosa es la historia de sus curiosidades, y la de las estupideces y extravagancias que se han ido acumulando a su alrededor, como ocurre con todas las celebridades.

Y, ¿quién es él?

Si se divide la longitud de una circunferencia cualquiera por la de su diámetro, se obtiene siempre el mismo cociente -un número cercano a 3,1416-, sin importar para nada que la circunferencia sea microscópica, o rodee todo el cosmos. Es una constante de la geometría de nuestro mundo euclidiano, tal vez la más importante de toda la ciencia, simbolizada por la letra griega pí desde 1737, año en que fue adoptado y puesto en uso público este símbolo por el matemático Leonhard Euler. La elección no fue arbitraria: se debió al hecho de ser precisamente pí la primera letra de la palabra perímetro en griego.

Esta proporcionalidad directa entre la circunferencia y su diámetro es una verdad que hoy conoce todo estudiante de secundaria, pero que los griegos tardaron más de dos siglos en establecer. Y quedó también establecida desde esa lejana época la proporcionalidad directa entre el área del círculo y el cuadrado del radio. En efecto, Hiparco de Chios encontró que el área de cualquier círculo era igual a una constante, que estimó en 3,16049, multiplicada por el cuadrado del radio.

Nadie conoce ni podrá conocer jamás el desarrollo decimal completo de pí. La razón estriba en que este número pertenece a una clase que los matemáticos llaman irracionales, números que tienen la propiedad de no poderse expresar como cociente de dos enteros. El desarrollo decimal de los números que, por el contrario, son cocientes o razón de dos enteros, llamados por ese motivo racionales, presentan, a partir de cierta posición, una periodicidad en sus cifras decimales que se repite indefinidamente. Basta, entonces, un cálculo elemental, y podemos predecir cualquiera de sus cifras, sin importar para nada lo alejado del lugar que le corresponda en el desarrollo, y sin necesidad de conocer las anteriores. Vale decir, a los números racionales, aunque algunos requieran infinitas cifras para escribirlos, los conocemos en su totalidad. Si, en cambio, quisiéramos ahora predecir una cifra determinada de pí, por su aperiodicidad infinita y por la falta completa de regularidad, sería necesario realizar el cálculo completo de todas sus cifras decimales hasta llegar a la posición deseada.

Las ideas anteriores pueden expresarse de otra manera: un número irracional, como es el caso de pí, no puede ser representado por medio de una expresión que contenga un número finito de operaciones elementales entre enteros (suma, resta, multiplicación, división y extracción de raíces cuadradas). En cierta forma, es una verdad inalcanzable por métodos finitos. O una verdad infinita, y por tanto divina e inexpugnable para los simples y finitos mortales.

Por muchos años se sospechó que pí era un número irracional. No obstante, hubo que esperar hasta 1761, año en el que Johann H. Lambert, matemático alemán, presentó a la Academia de Ciencias de Berlín la primera demostración. Unos años más tarde, el francés Adrien Marie Legendre le dio rigor a la demostración anterior y, adicionalmente, logró probar que el cuadrado de p gozaba de la misma propiedad.

El descubrimiento

En el principio pí era 3. Así consta en tabletas babilónicas, en papiros muy antiguos y en la Biblia. En el Libro III de los Reyes se puede leer: ” Hizo, además, un mar fundido, de diez codos de un borde al otro [el diámetro]. Era completamente redondo y tenía cinco codos de altura. Un cordón de treinta codos [tres veces el diámetro] ceñía toda su circunferencia”. En el Papiro de Moscú, documento de la decimosegunda dinastía egipcia (1890 a.C.), ya aparece una aproximación mejor: se toma para pí el valor 3,1605. En algunas tabletas babilónicas más recientes se ha encontrado la aproximación 25/8, o sea 3,125, un poco mejor que la anterior y suficiente, con seguridad, para satisfacer la generosa y descomplicada agrimensura de la época, de un mundo despoblado.

En 1858, un joven anticuario escocés, Henry Rhind, compró en Luxor un papiro que al descifrarlo reveló ser un manual práctico de matemáticas, copiado en el año 1650 a.C. por el escriba Ahmés. En uno de los problemas resueltos en el Papiro Rhind, nombre con el cual se lo conoce hoy, se propone la siguiente regla para calcular el área de un granero de base circular: retire 1/9 del diámetro y construya un cuadrado con el resto; el área de este último será el valor buscado. En términos modernos, esta cuadratura imperfecta del círculo equivale a tomar 3,16049… como valor de pí, aproximación aceptable para multitud de cálculos sencillos.

Una hoja del famoso papiro Rhind

Apolonio de Pérgamo, conocido en el mundo antiguo como El Gran Geómetra, y más respetado por sus contemporáneos que el mismo Euclides, halló la aproximación 3,1416, la versión más popular del número -el pí de los bachilleres y de la mayoría de sus padres-. Para infortunio de las matemáticas, se borraron todas las huellas del camino seguido por Apolonio, al desaparecer para siempre la mayor parte de su obra.

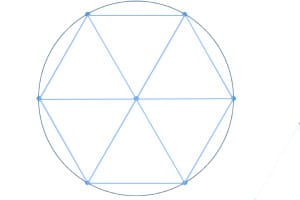
De todos los intentos realizados en la Antigüedad para determinar el valor de pí, el de Arquímedes -siglo tercero a.C.- fue sin ninguna duda el más serio y riguroso. Arquímedes intercaló o acotó la circunferencia entre dos hexágonos, uno inscrito y otro circunscrito, a los cuales les fue duplicando reiteradamente el número de lados hasta llegar a 96. La longitud de la circunferencia quedó, entonces, atrapada numéricamente entre los perímetros de los polígonos inscrito y circunscrito de 96 lados, de lo cual dedujo el siracusano que p debía estar situado entre los números 3,1408… y 3,1428… Años más tarde, Ptolomeo, el más célebre de los astrónomos antiguos, y propulsor del sistema geocéntrico que tantos dolores de cabeza costó a Copérnico y a Galileo, propuso para pí el valor 3,141666…, después de aproximar la circunferencia por medio de un polígono inscrito de 720 lados.

Los babilonios, 2.000 años antes de Jesucristo, obtuvieron para p el valor 3,25, por medio de un hexágono inscrito en un círculo de radio unitario

Hasta el Oriente antiguo y misterioso se propagó la urgencia por alargar a pí. En el siglo V, el matemático y astrónomo chino Tsu Chúng-Chih descubrió la aproximación 3,1415929, correcta hasta la sexta cifra decimal, y suficiente con holgura para realizar la mayoría de los exigentes cálculos requeridos por la ciencia actual. Increíble proeza geométrica que los científicos le premiaron bautizando con su nombre uno de los cráteres lunares. Nadie sabe aún cómo la logró, al perderse para siempre el libro que contenía los detalle de sus cálculos.

En Italia, Leonardo de Pisa, apodado Fibonacci, uno de los más célebres matemáticos del siglo XIII, encontró que pí debía estar situado entre los números 3,1410 y 3,1427. Y en el mismo siglo, su compatriota Dante Alighieri-¡quién podría imaginarlo!- propuso la aproximación 3 + /10, equivalente a 3,1414…, demasiado buena para cualquier poeta. En Arabia, un matemático del siglo XVI, conocido con el nombre de Al-Kashi, dio como valor de p el número 3,1415926538979, correcto hasta la novena cifra decimal.

Unos años más tarde, el alemán Ludolph van Ceulen, después de consagrar por entero su vida al cálculo de pí, logró elevar la cifra anterior a 35 dígitos, motivo por el cual en Alemania se conoce todavía a pí con el nombre de número ludolphiano. Van Ceulen, infatigable, utilizó un descomunal polígono de más de cuatro trillones de lados. Su viuda, en homenaje póstumo a la perseverancia infinita de su esposo, convirtió a pí en un número lapidario: como epitafio, en la tumba de su marido hizo grabar para siempre los treinta y cinco dígitos.

Los grandes físicos también se añadieron a la lista de los despectivamente apodados “cazadores de dígitos” y se involucraron en la competencia por alargar a pí. Huyghens obtuvo nueve decimales exactos con una economía increíble de recursos, pues no se valió más que del hexágono. Newton fue más lejos y calculó quince cifras decimales, para lo cual utilizó el desarrollo en serie infinita de la función arco seno; sin embargo, en lugar de sentirse orgulloso por semejante tarea, le confió a un colega suyo: “Me da vergüenza confesar a cuántas cifras llevé estos cálculos, que realicé por no tener otra cosa que hacer en aquel momento”.

En 1699, Abraham Sharp, un desconocido en el mundo matemático, utilizando series infinitas de rápida convergencia, duplicó sin esfuerzo el número de cifras obtenidas por Van Ceulen. Y en 1706, John Machin, valiéndose de los desarrollos en serie de la función arco tangente, logró obtener los cien primeros decimales de p. Un siglo más tarde, Johann Dase, calculista prodigio al servicio del matemático Carl F. Gauss, en sólo dos meses de trabajo llevó el desarrollo de p hasta la cifra doscientos cinco (Dase podía multiplicar mentalmente dos números de cien dígitos, proeza sobrehumana que le tomaba cerca de ocho horas, por lo que su cerebro puede muy bien considerarse el precursor de los modernos supercomputadores). Apareció luego en la historia de pí otro desconocido de apellido Richter: en 1854 elevó en forma espectacular la marca mundial a quinientos dígitos decimales.

El siguiente paso decisivo lo dio en 1873 el matemático británico William Shanks. Después de más de veinte años de pacientes y aburridísimos cálculos a mano, pulverizó, en apariencia, todas las marcas anteriores: logró desentrañar las primeras 707 cifras decimales de pí. Récord que a sus contemporáneos les pareció impresionante, sólo superado después de la aparición de las modernas máquinas de cálculo electrónico. Shanks analizó el resultado obtenido, y observó un hecho misterioso: había una clara deficiencia de sietes. En efecto, este dígito sólo aparecía 51 veces, mientras que cada uno de los nueve restantes lo hacía cerca de 70.

Apenas en 1946, y gracias al auxilio de las calculadoras mecánicas, se aclaró el misterio del siete deficitario. D. F. Ferguson probó que Shanks había cometido un error fatal al llegar al dígito de la posición 528. En consecuencia, las últimas ciento ochenta cifras, precisamente las que más gloria le habían dado, y también las más tediosas y difíciles de calcular, estaban equivocadas. Se perdieron con gran dolor varios años de trabajo. Su verdadero récord de resistencia bruta, 527 cifras correctas, era apenas superior al de Richter. Una vez corregido el error, el siete se hizo presente en la misma proporción de los demás números, un hecho notable e inesperado, de consecuencias teóricas trascendentales. Cosas importantes se derivarán más tarde de ahí. Especulaciones increíbles.

Al entrar a la era moderna de los computadores electrónicos, los cálculos anteriores se volvieron juego de niños y, de paso, hicieron que el récord de Shanks, como proeza manual, se eternizara: nadie, en los setenta y seis años que transcurrieron hasta hacer su aparición el primer computador electrónico tuvo el coraje suficiente para enfrentarlo a mano limpia.

En 1949, y después de setenta horas de trabajo continuo, un computador ENIAC, programado por el genial matemático húngaro John von Newmann, halló los 2.037 primeros decimales de pí. Un lujo -ociosidad para muchos- de la inteligencia humana, si se tiene en cuenta que con cuatro cifras decimales se resuelve la mayor parte de las necesidades geométricas de la vida corriente, con dieciséis se puede calcular un círculo de diámetro igual al de la órbita terrestre, con un error apenas inferior a un milímetro, y con cuarenta es posible calcular la circunferencia del universo conocido con una precisión tal, que el error cometido es inferior al diámetro de un átomo de hidrógeno.

No obstante las burlas de algunos, el número ludolphiano, aunque elusivo, siguió alargándose. En 1958, la marca mundial se elevó dramáticamente a 40.000 dígitos. La velocidad de los computadores continuó aumentando de manera vertiginosa y con ello fueron brotando en cascada nuevas cifras. En 1961, ocho horas de cálculos en un IBM 7090 permitieron conocer las primeras 100.265 cifras. Por una rara coincidencia del destino, uno de los ingenieros responsables del programa era el doctor Daniel Shanks, sin ningún parentesco con aquel otro Shanks que calculó a mano las primeras 707 cifras.

La marca del primer millón de cifras decimales se superó al fin en 1973. El honor correspondió a los investigadores J. Guilloud y M. Bouyer; y la responsabilidad recayó esta vez en un computador CDC7600, que realizó los cálculos en menos de un día. Con esta nueva marca quedó cerrada decorosamente la era de los métodos clásicos. De no obtenerse algoritmos radicalmente diferentes, sería lento y penoso el ascenso por la escalera infinita de pí, y habría que confiarlo principalmente a las siempre crecientes velocidad y eficiencia de los nuevos equipos de cómputo.

La era Ramanujan

Una de las mentes más asombrosas y desconcertantes que jamás haya existido la poseyó un hindú, de origen humilde, autodidacta por obligación y matemático por predestinación celestial, llamado Srinivasa Ramanujan. Por su formación netamente autodidáctica y fuera de toda la tradición lógica de occidente, los métodos de su razonamiento se movían entre el misterio absoluto y la intuición más profunda. Los resultados obtenidos, que lindan con el milagro, los atribuía Ramanujan a revelaciones que en sueños le hacía la diosa Namakkal. Contaba que, al levantarse por la mañana, escribía con premura los teoremas soñados, aunque no siempre resultasen correctos. El caso Ramanujan lo resume James Newman de la siguiente manera: “Así, sin más ayuda que sus facultades, logró reproducir un fructífero medio siglo de matemáticas europeas. Sin duda, nunca había sucedido un hecho tan prodigioso en la historia del pensamiento”.

Srinivasa Ramanujan poseyó una de las mentes más extrañas y prodigiosas que registra la historia de la ciencia. Gracias a sus descubrimientos hoy conocemos varios millones de cifras decimales de pí

Nadie habría imaginado que en el tesoro de Ramanujan, su cuaderno de notas, encontrado después de su muerte prematura a los 35 años de edad, se hallaba escondida la clave del algoritmo que habría de empequeñecer todas las marcas anteriores en el cálculo de pí: la teoría de ecuaciones modulares. Fue esta herramienta de alto nivel la que sirvió a los hermanos Jonathan y Peter Borwein para emprender a comienzos de la década del ochenta un asalto definitivo a la fortaleza de pí. Armados de la poderosa teoría de Ramanujan y de la teoría de integrales elípticas, en una alquimia matemática refinadísima, lograron desarrollar varios algoritmos iterativos (aquellos en los cuales los resultados de un ciclo sirven de alimentación para el siguiente) de ultrarrápida convergencia, alguno de ellos ya anticipados por el genial hindú.

En enero de 1986, David H. Bailey obtuvo el primer éxito sensacional con los algoritmos desarrollados por los Borwein. Al combinarlos con novísimas técnicas para multiplicar grandes números, y provisto de un supercomputador CRAY-2, llevó los cálculos hasta la cifra 29’360.000. Se calculó en doce billones el número de operaciones aritméticas requeridas por el algoritmo de cálculo, y demandaron veintiocho horas de proceso.

Un año después, el japonés Yasumasa Kanada, respaldado por artillería pesada, esta vez representada por el método iterativo desarrollado por los Borwein, y contando con la ayuda de un poderoso NEC SX-2, estableció la marca de 134’217.000 cifras decimales. Un año más, y el mismo Kanada, esta vez auxiliado por un supercomputador Hitachi, llevó el desarrollo hasta la cifra 201’326.000. Justo al comenzar la década del 90, el cálculo fue llevado hasta los mil millones de cifras, para saltar de ahí, en 1995, a 3.200 millones. Por último, en 1997, Kanada vuelve a superar su propia marca mundial y la fija en un poco más de 51 millardos. Un récord que aturde y que debe tener a Van Ceulen revolcándose en su tumba. Para escribir los resultados en forma completa se requeriría, no ya una lápida, sino toda una biblioteca de más de quince mil volúmenes.

El japonés Yasumasa Kanada

Quedó así apenas inaugurada la millonaria era de Ramanujan. Llegar a los cien millardos de cifras decimales es ahora una meta realizable a corto plazo, y el billón de cifras ya no asusta a los teóricos. ¿Qué seguirá de ahí? Estamos apenas en las puertas de la nueva era y ya la imaginación ha sido desbordada, pero no la inagotable curiosidad humana.

Vale la pena destacar que en la actualidad, el cálculo de los primeros miles de cifras de pí se ha convertido en rutina obligada para probar la confiabilidad, grado de complejidad y velocidad de cómputo de los nuevos equipos electrónicos. Escribe el experto Philip J. Davis: “El misterioso y maravilloso número pí se ha visto reducido a un gargarismo con el que las máquinas de calcular se aclaran la garganta”. Una triste realidad: lo que los cerebros humanos, de carbono, hicieron todos juntos en cientos de años, los cerebros de silicio lo repiten hoy en centésimas de segundo.

Presencia insólita de Pí

Por su misma definición, relacionada en forma íntima con el círculo, es de esperar que el número pí intervenga en los problemas geométricos relacionados con ángulos, círculos, esferas, conos, cilindros, sólidos de revolución, elipses, elipsoides… Y en efecto, así es: en todas las fórmulas para calcular las superficies y los volúmenes de dichos sólidos aparece pí.

Pero rápidamente el número pí trasciende el ámbito natural de lo geométrico y se entromete en el análisis. Allí lo encontramos, de repente, desempeñando papel protagónico en los sitios más inesperados y raros. Por ejemplo, es bien conocida la fórmula de Stirling

aproximación que permite hallar rápidamente y en forma aproximada el valor de factorial de n, escrito n!, cuando n es grande (n! se define como el producto de todos los enteros entre 1 y n ; y la letra e representa un número cercano a 2,7, base de los logaritmos llamados naturales).

El prolífico matemático Leonhard Euler encontró que, entre la función exponencial de base e y exponente complejo, y las funciones circulares seno y coseno, existía una relación directa y sencilla. De ella obtuvo la igualdad epii + 1 = 0, relación que hoy a todos los matemáticos les parece elemental y completamente natural, pero que para los contemporáneos de Euler era algo que desbordaba los límites de lo posible: puro arte de brujería. Fue tal la admiración que sintieron por ella, que llegaron a proclamarla la fórmula más bella de toda la matemática, ya que hacía intervenir solidariamente, y de una forma simple y elegante, los cinco números más importantes: por un lado, las dos constantes enteras de mayor popularidad, el uno y el cero; por el otro, la unidad imaginaria i (“la imposible raíz cuadrada de -1″, en palabras del matemático Felix Klein), junto a las dos constantes irracionales y trascendentes más notables, pí y e. Asimismo, utilizaba las dos relaciones matemáticas más comunes e importantes: suma e igualdad. No se puede pedir más.

En la física, pí aparece también con generosidad. Desde las fórmulas para calcular las fuerzas de atracción o repulsión entre cargas eléctricas o entre masas magnéticas, hasta aquellas que describen el fenómeno de difusión de un soluto en un solvente, pasando por las importantes fórmulas del electromagnetismo, o por las del movimiento armónico simple -entre ellas la del péndulo-, y por las de todos los problemas de cuerpos en rotación. Hasta en los meandros de los ríos se sumerge pí: el río serpentea y se apereza pí veces más de lo necesario, de tal modo que si medimos su recorrido por un valle y luego dividimos este valor por la distancia más corta que podría recorrer si fuera eficiente, obtenemos precisamente pí. La escueta realidad es que no hay rincón de la ciencia en que no encontremos su sombra.

¿Quién podría sospechar, basándose únicamente en la definición, que p aparecería en la fórmula que sirve a los estadísticos para describir y predecir los errores cometidos al medir la longitud de una barra, el diámetro de un tornillo o la cantidad de hilo contenido en un carretel? Efectivamente, éstos y otros fenómenos de naturaleza semejante pueden describirse por medio de la llamada distribución normal o campana de Gauss:

Y si se trata de explicar y describir el movimiento errático de una partícula en un fluido -movimiento Browniano-, la fórmula correspondiente, descubierta por Einstein, también contiene pí.

Normalidad de Pí

Una de las características más notables observadas en el desarrollo decimal de pí, al menos en la parte analizada, esto es, en los primeros seis mil millones de cifras, es que los diez dígitos se reparten en él de manera uniforme; es decir, cada uno de ellos aparece aproximadamente seis millones de veces. Y lo mismo ocurre cuando en lugar de dígitos individuales se toman parejas de números consecutivos: cada una de ellas, desde la 00 hasta la 99, aparece aproximadamente el mismo número de veces. De igual modo, se han examinado todas las ternas y cuaternas de dígitos consecutivos que pueden formarse, y siempre se ha encontrado la misma misteriosa regularidad.

El hecho de que los dígitos del cero al nueve se repartan uniformemente a lo largo del desarrollo decimal de un número, no impide que en ciertos tramos se presenten rachas continuas o predominio local de uno o varios de los dígitos. Se conocen en el desarrollo de pí, por ejemplo, una racha de doce nueves consecutivos, dos de ocho sietes y una de nueve sietes. En realidad, la uniformidad sólo aparece cuando se toma una sucesión suficientemente extensa. Es una propiedad que se manifiesta e interesa sólo a largo plazo.

A todo número real cuyos dígitos en una base de numeración dada presente la característica de uniformidad atrás mencionada, se lo llama normal en esa base. La normalidad en una base es la primera y principal condición que debe cumplir una tabla de números para considerarse aleatoria. Se conjetura que pí es un número normal en base diez; sin embargo, nadie hasta el momento ha sido capaz de probarlo, pero la evidencia estadística se inclina prometedoramente en favor de la hipótesis.

La insondable e infinita sabiduría de Pí

Aceptando que la propiedad de normalidad que exhibe la parte conocida de pí se extienda en forma indefinida, y que dicha normalidad esté correlacionada, como es de esperar, con cierta aleatoriedad, aunque débil, puede conjeturarse seriamente que en él está encerrada toda la sabiduría del universo. Es una atrevida especulación teórica, no una broma.

Un ejemplo vale por mil palabras. Es posible codificar numéricamente un texto cualquiera al sustituir cada letra o signo de puntuación por medio de un número previamente convenido. Podemos, por ejemplo, remplazar cada letra por un número de dos dígitos que indique su posición dentro del abecedario: la A por el 01, la B por el 02… la Z por el 27, el espacio en blanco por el 00 y los signos de puntuación por números del 28 en adelante. Según este código, el comienzo de la primera frase de El Quijote, “EN UN LUGAR”, se convertiría en el número N= 0514002214001222070119.

Pues bien, en algún lugar de pí, con seguridad muy distante, debe encontrarse la secuencia N anterior. En realidad, lo que se puede afirmar es que si pí es normal en base diez, entonces es altamente probable que la secuencia representada por N aparezca intercalada en algún lugar de su infinito desarrollo decimal. En términos prácticos, la normalidad de p significa que podríamos apostar una suma muy alta a que en él encontraremos, tarde o temprano, el número N. Y lo dicho sobre N lo podemos decir de cualquier otro número, sin importar lo grande que sea, y sin importar tampoco que nuestro sentido común lo rechace.

Si con santa paciencia codificásemos de la manera anterior todo El Quijote, obtendríamos un entero Q de varios millones de dígitos, inmenso cuando se lo mide respecto a la modesta escala humana, pero nada, absolutamente nada, si se lo compara con la inmensidad infinita del desarrollo completo de pí. Con iguales argumentos a los presentados atrás, lo más probable es que dicho número también se encuentre intercalado en alguna zona, con seguridad muy remota, del desarrollo decimal. En esencia, es el mismo problema del chimpancé que golpea eternamente las teclas de la máquina de escribir: al esculcar sin afanes en el montón astronómico de hojas mecanografiadas, algún día de suerte nos tropezaremos con el texto de El Quijote. Eso sí, el tiempo que habría que gastar en esa experiencia se sale de cualquier escala imaginable. Para ser exactos, se requeriría disponer de una paciencia sobrehumana y del ocio eterno de los dioses.

Lo que acabamos de afirmar de El Quijote, también lo podemos afirmar de cualquier otro libro que se haya escrito, en español o en cualquier otro idioma, por raro que éste sea. Intercalado en alguna parte muy remota de pí, deberemos encontrarlo. Es así altamente probable que también encontremos en él lo que Jorge Luis Borges imagina en su Biblioteca de Babel, generada al permutar de todos los modos posibles los caracteres utilizados en la escritura: “Todo: la historia minuciosa del porvenir, las autobiografías de los arcángeles, el catálogo fiel de la biblioteca, miles y miles de catálogos falsos, la demostración de la falacia de esos catálogos, la demostración de la falacia del catálogo verdadero, el evangelio gnóstico de Basílides, el comentario de ese evangelio; el comentario del comentario de ese evangelio, la relación verídica de tu muerte,…”. En Borges es ficción, en pí es una seria posibilidad teórica.

Es una posibilidad alucinante el hecho de que en alguna parte de la expansión decimal de pí se encuentre almacenado el relato minucioso de nuestra propia muerte, y los detalles íntimos y secretos de toda nuestra vida, contados en prosa y en verso, en todos los idiomas conocidos. Y los códigos genéticos de todas las especies vivas, y todos los descubrimientos científicos, todos los poemas escritos y los que se habrán de escribir, toda la literatura musical. Y las obras completas de todos los premios Nobel de literatura, y las obras no escritas aún de los que serán nominados en los años futuros. La Galaxia Gutenberg completa, según expresión afortunada de Henri Broch. Todos, absolutamente todos los conocimientos adquiridos por la especie humana, y los que se habrán de obtener en el futuro, deben reposar en silencio, allá, en segmentos remotísimos, inexplorados e inexplorables de p. En fin, es impresionante y maravillosa la posibilidad teórica de que toda la sabiduría del universo pueda encontrarse allí, en secreto, congelada, en un objeto abstracto y de apariencia tan inofensiva y simple como lo es la relación entre cualquier circunferencia y su diámetro.

Sin embargo, apacigüemos nuestras esperanzas: desde el punto de vista práctico, nada hay útil en esa sabiduría. Aunque conociésemos trillones de trillones de dígitos de pí, la posibilidad de hallar en ellos algún texto sensato y de utilidad es infinitamente pequeña, ya que la información está diluida hasta alcanzar niveles de densidad inimaginablemente pequeños. Podría ser pí un recipiente inagotable de conocimientos y, quizá por esa misma razón, completamente inútil. No hay ninguna antinomia en esto, pues su locuacidad es interminable: así como figura una historia verdadera, aparecen también, para confundirnos, todas las posibles versiones falsas: todas las deformaciones de la verdad suministradas por el maquiavélico arte combinatorio. Y no existe ninguna manera sencilla de distinguirlas. Como oráculo para adivinar el porvenir, es más vago que el I Ching y que todos los libros esotéricos de profecías medioevales, como bien lo dice Martin Gardner. Y responde insoportablemente mucho más de lo que se le pregunta. Peca pí por exceso: podría contener demasiados conocimientos.

Por ser pí una constante geométrica del universo, deducible teóricamente a partir de postulados simples, experimentables en regiones euclidianas, de gravedad moderada, como son precisamente aquellas que son propicias para la germinación de la vida, donde quiera que existan seres inteligentes con culturas suficientemente avanzadas, es posible que ya sean conocedores de él. Además, la idea de acotarlo entre polígonos inscritos y circunscritos de lados que crecen y crecen en número, es elemental e inmediata, repetible con facilidad en otros mundos inteligentes. En consecuencia, para revelarnos su presencia o revelarles la nuestra, el número pí, codificado o expresado de alguna manera que resulte universal, podría ser el vehículo ideal.

Final

Es frondosa y fascinante la historia del número misterioso. Con el paso del tiempo y el esfuerzo continuo de los hombres se le han restado misterios y se ha ampliado el panorama que tenemos de él, pero han quedado y quedarán siempre cosas importantes por averiguar. Su carácter de inconmensurable o irracional obliga a que sea así: lo vuelve, en cierta forma, infinito, o invulnerable a la comprensión total y perfecta, insondable. No olvidemos esta melancólica verdad: los humanos pensamos con un cerebro que, aunque prodigioso, no es, en el fondo, más que una complicadísima máquina de estado finito, en el sentido que los ingenieros de sistemas dan a este término. Y sus poderes son también finitos. La comprensión completa de pí los rebasa con holgura.

Al llegar a este párrafo final, y cuando ya se han dicho tantas cosas sobre el enigmático pí, surgen algunas preguntas inquietantes. ¿Cuál es el pasadizo subterráneo que lo comunica con casi todos los fenómenos del mundo? ¿Cuál es el hilo sutil que lo conecta con hechos tan dispares? ¿Cuál es la razón profunda y secreta para que sea precisamente él y no otro número real? Nadie tiene aún respuestas definitivas. Y tal vez sea preferible cultivar un poco la oscuridad para que el misterio sobreviva.

ENLACE CON LA NOTA ORIGINAL:

http://blogs.elespectador.com/catrecillo/2015/03/14/la-insondable-sabiduria-de-pi/

ANTONIO VÉLEZ: 

Nació en Medellín, Colombia, en 1933. Es ingeniero electricista, egresado de la Universidad Pontificia Bolivariana, de Medellín, y máster en matemáticas de la Universidad de Illinois, en Estados Unidos.

Por varios años fue profesor de tiempo completo en el área de matemáticas, en varias universidades colombianas. Durante una década estuvo vinculado al Departamento de Investigación Operativa de la empresa Coltejer (Colombia). En tiempos presentes escribe artículos para la revista de abogados editada en Bogotá: Legis y trabaja en la universidad EAFIT.

Ha publicado, entre otros, los siguientes libros:

Álgebra Moderna, Universidad de Antioquia, Medellín, 1989; ISBN 958-9021-7-6;

El hombre, herencia y conducta, Editorial Universidad de Antioquia, Medellín, 1990, segunda edición, ISBN 958-9021-7-6.

De Pi a pa: ensayos a contracorriente, Lengua de Trapo, Madrid, noviembre del 2002, ISBN 84-89618-99-2.

Del big bang al Homo sapiens, Universidad de Antioquia, Medellín, tercera edición, 2004, ISBN 958-8160-68-5.

Homo sapiens, Villegas Editores, Bogotá, 2006, ISBN 978-958-8293-70-7.

Pensamiento creativo (con Ana Cristina Vélez y Juan Diego Vélez como coautores), Villegas Editores, Bogotá, agosto de 2010; ISBN 978-958-8293-70-7.

Creatividad e inventiva. Retos de siglo XXI (con Ana Cristina Vélez como coautora), Editorial Universidad de Antioquia, Medellín, febrero de 2013, ISBN 978-958-714-546-5.